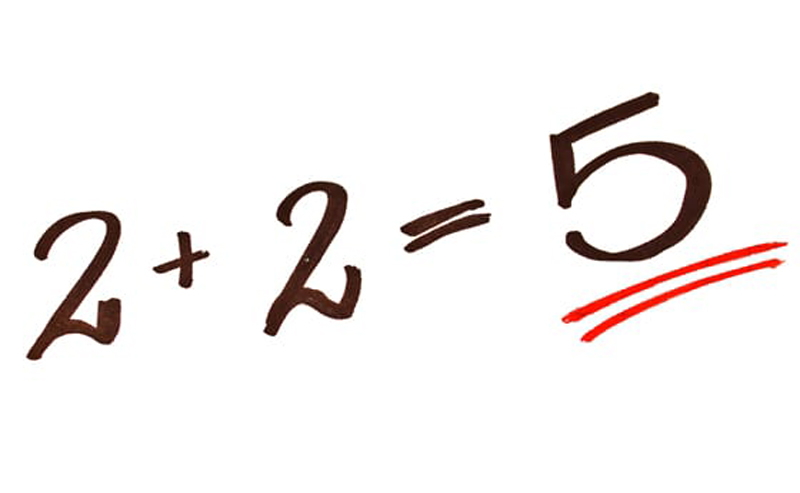
2 +2 = 5
José Ángel Pérez

Monterrey.- Las deducciones válidas son aquellas que proceden de un razonamiento lógicamente consistente. Los Elementos, de Euclides, son un ejemplo de esta consistencia, ya que sólo con cinco postulados, 5 nociones comunes y 23 definiciones, contenidas en el Libro Primero, construye toda la geometría contenida en los 13 libros que componen Los Elementos, que aún hoy se enseña en las escuelas básicas, por responder a una realidad inmediata. Euclides nos enseña una manera lógica de razonar para obtener demostraciones válidas. Pero, ¡cuidado! Es muy importante partir de postulados lógicos.

La matemática enseña una forma de razonar que no tiene por qué ser sosa, difícil o aburrida. Bertrand Russel, filósofo y matemático inglés, utilizó el famoso enunciado 2+2=5, como base para explicar que es posible demostrar cualquier propiedad si se comienza con una proposición falsa.
Se cuenta que cuando el gran matemático estaba hablando sobre esto en una conferencia, alguien de los asistentes le gritó desde su lugar:

¿Quiere usted decir que si 2 + 2 = 5, entonces es usted el Papa?

Efectivamente –contestó Russel; y comenzó a demostrarlo.
Postulado: 2+2=5

Proposición: yo soy el papa
Si 2+2= 5

Restemos 3 de cada lado de la igualdad y tenemos
1=2

Entonces, por simetría o ley de la conmutatividad
2=1

Si el papa y yo somos dos personas distintas y dado que 2=1

El papa y yo somos uno.

Resultado:
Yo soy el Papa.

Los elementos de Euclides y su quinto postulado dieron origen, más de dos mil años después, al surgimiento de las Geometrías no Euclidianas, bella forma de razonar y de encontrar otras realidades. Sin embargo, el razonamiento lógico no debe perderse y el partir de postulados aceptados por la razón.

Considero que algunos funcionarios de todos los niveles deberían leer a Euclides, Lobachebsky, Riemman y Poincaré, porque en sus estudios básicos, debieran haber estudiado sus fundamentos, no importa qué carrera eligieron al final y se evidencia que no lo hicieron. Esa es la explicación de por qué postulan tantas estupideces y, lo que es peor, ni siquiera las demuestran.